8 Correlatie tussen Twee Continuë Variabelen
samenwerken, betrouwbaarheidsinterval, effect size, open onderwijsbron, open studiebeurs, open wetenschap
Om de relatie tussen twee continue variabelen te kwantificeren, is de meest gebruikelijke methode het gebruik van een Pearson correlatiecoëfficiënt (aangeduid met de letter \(r\)). De Pearson correlatie neemt de covariantie tussen een continue onafhankelijke (\(X\)) en afhankelijke (\(Y\)) variabele en standaardiseert deze door de standaarddeviaties van \(X\) en \(Y\),
\[ r = \frac{\text{Cov}(X,Y)}{S_{X} S_{Y}}. \]
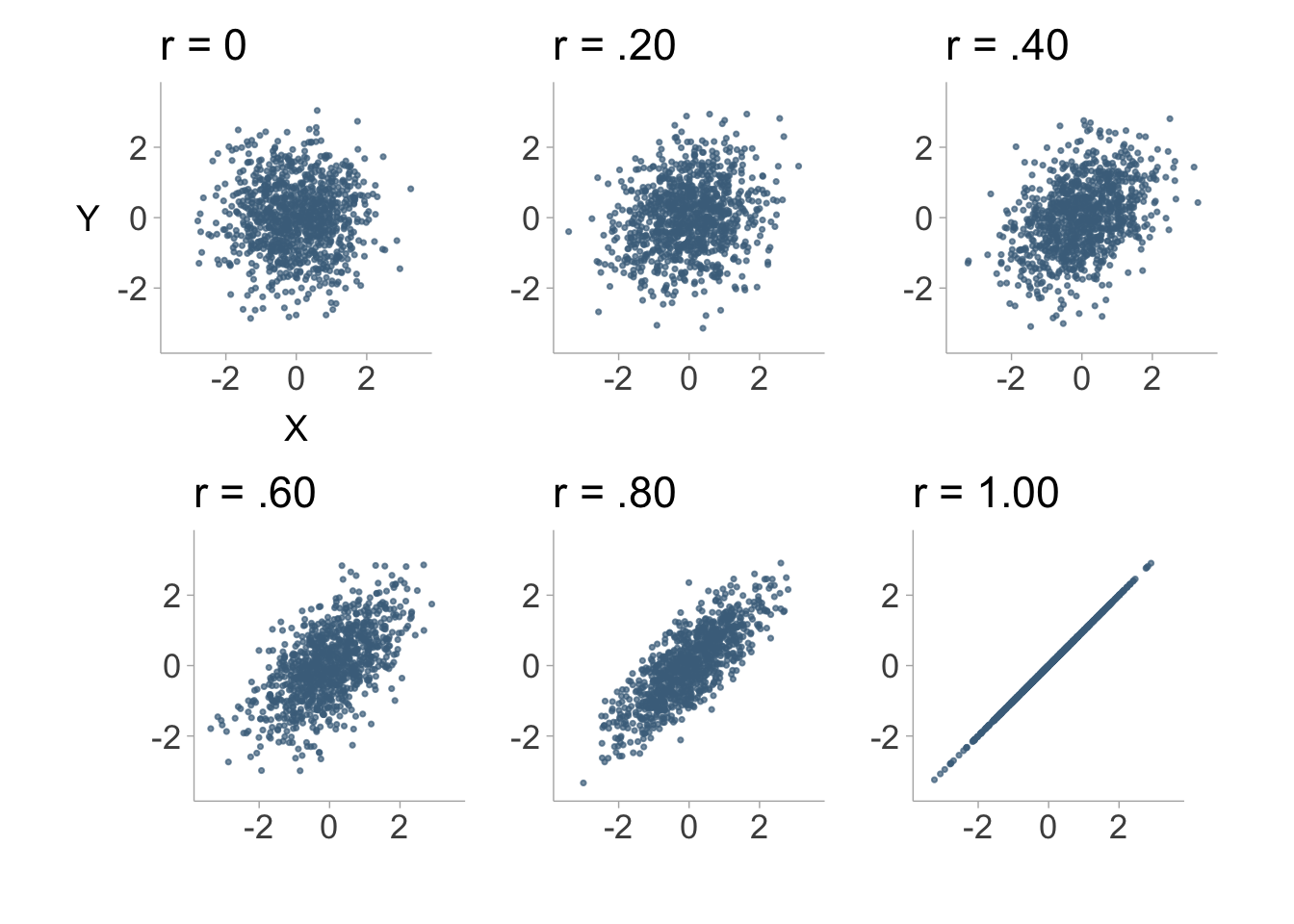
We kunnen visualiseren hoe een correlatie tussen twee variabelen eruitziet met scatterplots. ?fig-cor-voorbeeld toont diagrammen met verschillende niveaus van correlatie.

De standaardfout van de Pearson correlatiecoëfficiënt is,
\[ SE_r = \sqrt{\frac{\left(1-r^2\right)^2}{n-1}} \]
In tegenstelling tot Cohen’s \(d\) en andere maatstaven voor de effectgrootte, wordt de correlatiecoëfficiënt begrensd door -1 en positief 1, waarbij positief 1 een perfect positieve correlatie is, -1 een perfect negatieve correlatie is en nul aangeeft dat er geen correlatie is tussen de twee variabelen. De begrenzing heeft tot gevolg dat het betrouwbaarheidsinterval asymmetrisch is rond \(r\) (als de correlatie bijvoorbeeld positief is, ligt de ondergrens verder weg van \(r\) dan de bovengrens). Het is belangrijk op te merken dat bij een correlatie van nul het betrouwbaarheidsinterval symmetrisch en ongeveer normaal is. Om de betrouwbaarheidsintervallen van \(r\) te verkrijgen, moeten we eerst een Fisher’s Z-transformatie toepassen. Een Fisher’s Z transformatie is een hyperbolische arctangens transformatie van een Pearson correlatiecoëfficiënt en kan als volgt berekend worden,
\[ Z_r = \text{arctanh}(r) \]
De Fisher Z-transformatie zorgt ervoor dat \(Z_r\) een symmetrische en ongeveer normale steekproefverdeling heeft. Hierdoor kunnen we het betrouwbaarheidsinterval berekenen uit de standaardfout van \(Z_r\) (\(SE_{Z_r} = \frac{1}{\sqrt{n-3}}\)). We kunnen het betrouwbaarheidsinterval ook terugtransformeren naar een Pearson correlatieschaal,
\[ CI_{r} = \text{tanh}(Z_r \pm 1.96\times SE_{Z_r}) \]
We kunnen dan de boven- en ondergrens terugtransformeren naar de boven- en ondergrens van \(r\) door de hyperbolische tangens te nemen (het omgekeerde van de arctangens).
In R kan het volledige proces voor het verkrijgen van betrouwbaarheidsintervallen vrij eenvoudig worden uitgevoerd. Als je ruwe gegevens hebt voor \(X\) en \(Y\), dan kun je de correlatie berekenen met basis-R, cor(X,Y).
# example: r = .50, n = 50
r <- .50
n <- 50
# compute Zr
Zr <- atanh(r)
# calculate standard error of Zr
SE_Zr <- 1/sqrt(n-3)
# compute confidence interval of Zr
Zlow <- Zr - 1.96 * SE_Zr
Zhigh <- Zr + 1.96 * SE_Zr
# backtransform CI of Z to CI of Pearson correlation
rlow <- tanh(Zlow)
rhigh <- tanh(Zhigh)
# print pearson correlation and confidence intervals
data.frame(r = MOTE::apa(r),
rlow = MOTE::apa(rlow),
rhigh = MOTE::apa(rhigh)) r rlow rhigh
1 0.500 0.257 0.683De uitvoer laat zien dat de correlatie en de betrouwbaarheidsintervallen \(r\) = 0,50, 95% CI [0,26, 0,68].
